엇그제 일요일 동창들과 자전거로 여의도-김포-아라뱃길갑문 약 45km 편도 갔습니다.

수학 학원을 하는 친구와 앞서거니 뒤서거니 하며 가면서 제가 고문를 했습니다.

수학의 세계에서 실생활에 적용되는것이 많은데 뭐가 있겠니?? 등등.

저는 행렬을 예로 들어 이야기를 먼저 했습니다.

수학책의 맨 뒤에 나와서 별로 흥미도 없고, 실생활에 쓸모도 없을것 같은 행렬이

복잡한 다각형(토지의 도면인 지적도를 보면 대부분 다각형 입니다 - 저의 홍천 땅도 10각형)

의 면적을 아주 쉽게 계산하는 것을 보고 놀랍다고 했습니다.

학교에서는 왜 그런 이야기를 안했는지, 아니면 책에 있는데 내가 몰라서 아마 모르고(기억 x)

지나쳤는지도 모른다고요. 친구는 그 면적 이야기를 듣더니 그 내용은 교과서에는 안 나오고,

교과서 외의 내용으로 가르친다고(학원) 하면서 무슨 외국인 이름을 대더군요. 

포물선에 대하여 물어(시험) 봤습니다.

준선을 긋고, 한점에서 같은 거리에 있는 점의 집합이 포물선이다 등으로 정의를 설명하더군요.

나는 박박을 했죠.

이 정의는 나중에 문장을 만든것이다. 즉 이차 함수를 공부하다가 어떤 특이한 현상이 생기는

포인트(특이점)을 발견하고, 이 점으로 부터 만들어지는 특별한 이차함수를 포물선이라고

하고 이 곳선과 특이점의 관계를 함축적으로 설명한 것이 포물선이다고.

어떤 환경(수학및 물리(자연)에서 선,면,점,시간)에서 아주 특정한 조건에서 특별한

상태가 되는 것이 수학에서 답을 풀었다고 하는 것인데, 우리가 그동안 배운 산수와 수학은

모두 특별한 조건을 구한거지요(5000원 물건사고, 만원 내면, 5000원 거스름이라는 단

한가지의 특별한 해)

포물선은 특별한 해중에서 특별합니다.

이차방정식의 해의 공식인 (-b +- 루트 b제곱 - 4ac) / 2a 만큼 강력한 효과를 내지요

우리가 눈을 통해 세상을 볼수있고, 카메라로 그 순간을 오래 지속시킬수 있고,

대포가 어디에 떨어질지 알수도 있고(자유낙하 공식 s=1/2 gt제곱 에서 t의 제곱항만 있고 t항의 상수는 0),

스카이 tv위성 안테나를 작게 만들수도 있으니까요

y=ax제곱 + bx + c 에서 b=0 이면 포물선이 됩니다.

1시간전에 b의 값에 대하여 생각헤 봤습니다. b가 0이 아니면 포물선이 안됩니다.

이런 생각이 들었습니다.

b=0 이 아닌 곡선에 혹시 어디에 특이한 점이 있지 않을까???

아마 타원일지도 모르겟습니다......

-

9시40분 추가

타원은 폐곡선이고,  이차 함수는 개곡선(개곡선 맞나 아무튼 폐곡선 아님)이라서 반쪽(좌우의 반쪽도)만 생각한 것입니다.

타원의 모양이 좌우(상하) 같은 모양이라....

타원은 아니네요. 혹시 쌍곡선이라면 모를까...(타원은 폐곡선이라 중간에 수평(수직)선이 존재할수 밖에 없는데,

이차함수에서는 수직(수평)선은  잘 안나오니까요(x=0 인 특이점 빼고, ax제곱이 -bx 과 같을때 등 빼고)

-

11시30분 추가.

포물선의 특징인 '포물선의 모든 위치에서의 미분(곡선의 기울기)이 수직선은 수평입사선과 촟점의 정중앙'이라는 내용을 사족으로 넣습니다^^

포물면에 수평으로 입사하는 직선이 포물면에서 반사되면(기울기에서 입사각과 반사각이 동일하게) 모두 촛점을 지나는 내용입니다.

 

문득 굴절 주경의 경우가 생각납니다. 그동안 포물선(면)을 반사경으로만 생각해 왔기때문입니다.

당연히 굴절에서도 이 원리(포물)가 적용되는 줄 알았는데, 한번도 깊게 계산해 보지 않았습니다.

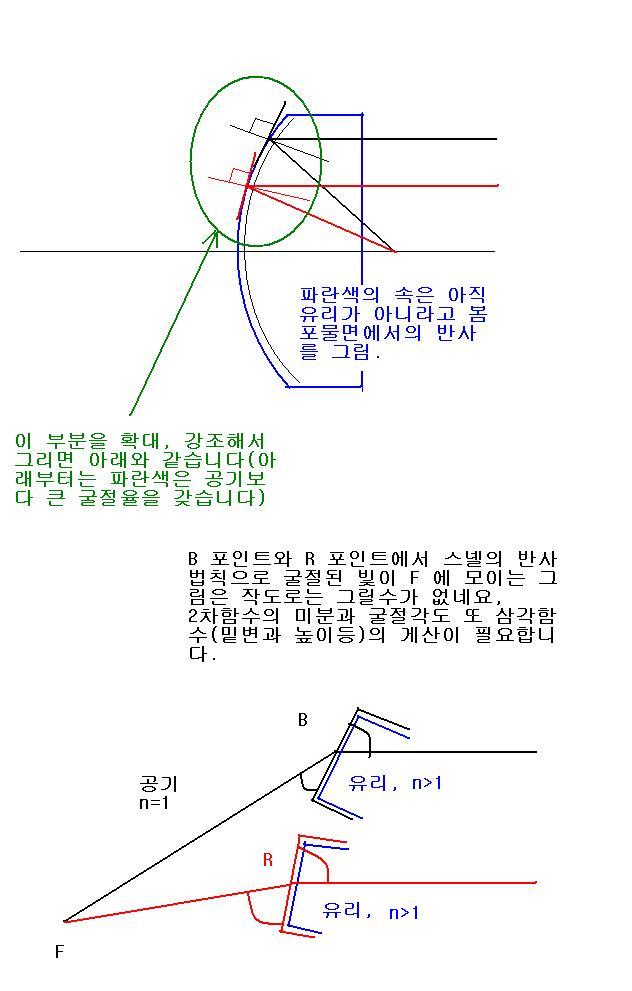
굴절 주경을 단순히 해서(한면은 평면, 다른 한면은 포물면) 머리속에서 그림 그리며 생각해 보겠습니다 

작도를 해보면 쉽게 풀릴것도 같고요.

-

15시25분 추가.

낮에 버스타고 외출을 하면서 생각해보니, 아래의 그림처럼 쉽게 작도할수가 없었습니다.

제가 미분책을 들춰보고 풀어도 저는 증명을 할 수 없을겁니다(즉 맞는지 안 맞는지, 포물면이지만 굴절에서는 촛점이 없을수도 있는지 모름..) ㅊㅊㅊ.

그러니 주경의 굴절유리가 포물면은 아닐지도 모릅니다^^ 

누가 책이나 카다로그에서 주경의 유리가 포물면 가공된것 보면 알려줘요(실제에서는 색수차문제가 있지만, 단색용 포물면이 있는지)

 

-

21시38분 추가

저녁 먹고 끙끙 거립니다.

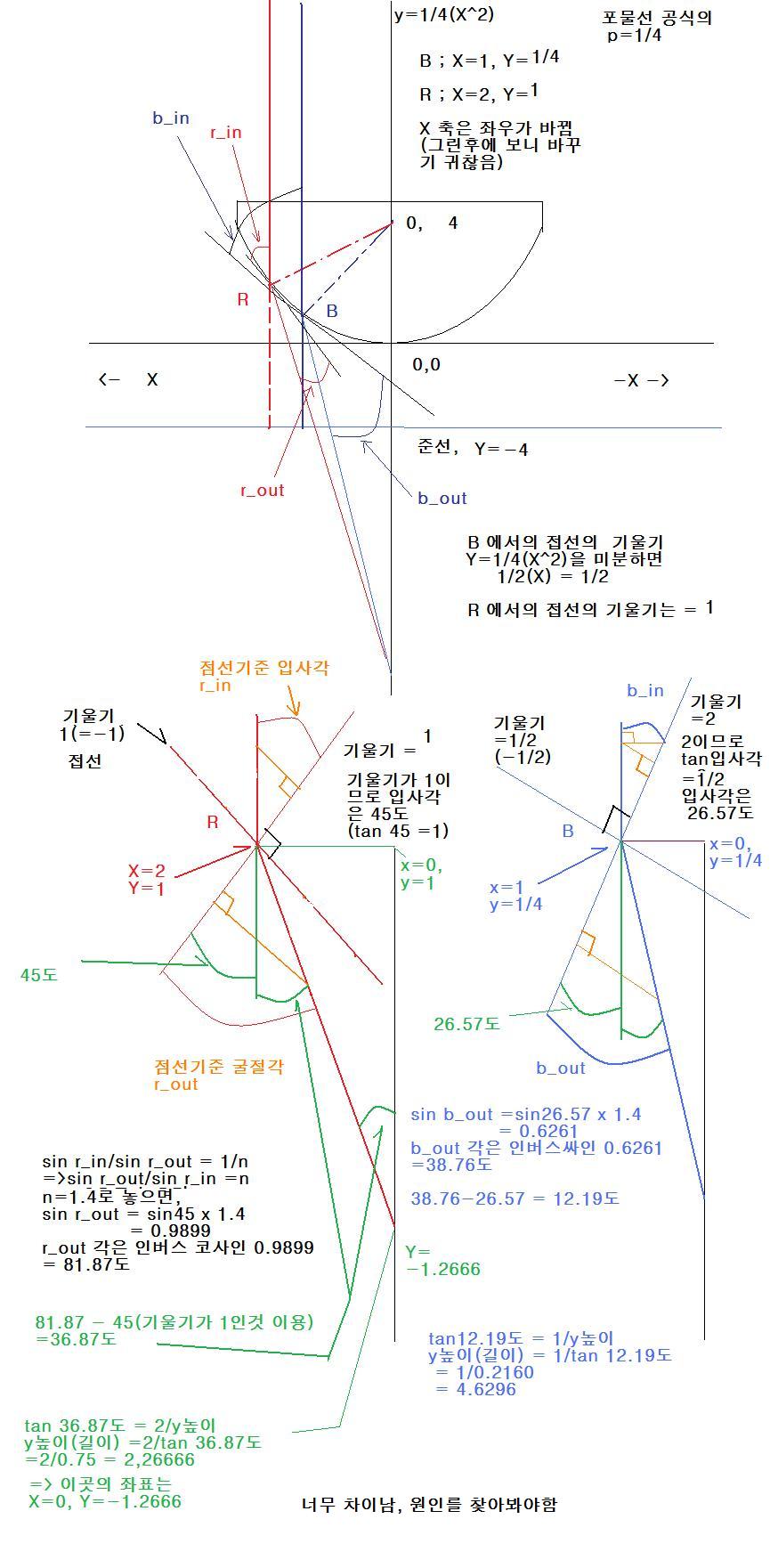
일단 스넬의 법칙(굴절 법칙)과 포물선의 2포인트에서 굴절되는 것만 작도 해보는데,,,,,

촛점이 안맞습니다.

뭐가 잘못된것인지 출력해서 봐야 겟습니다.... 혹시 굴절면은 포물면이 아닌가????

 

-

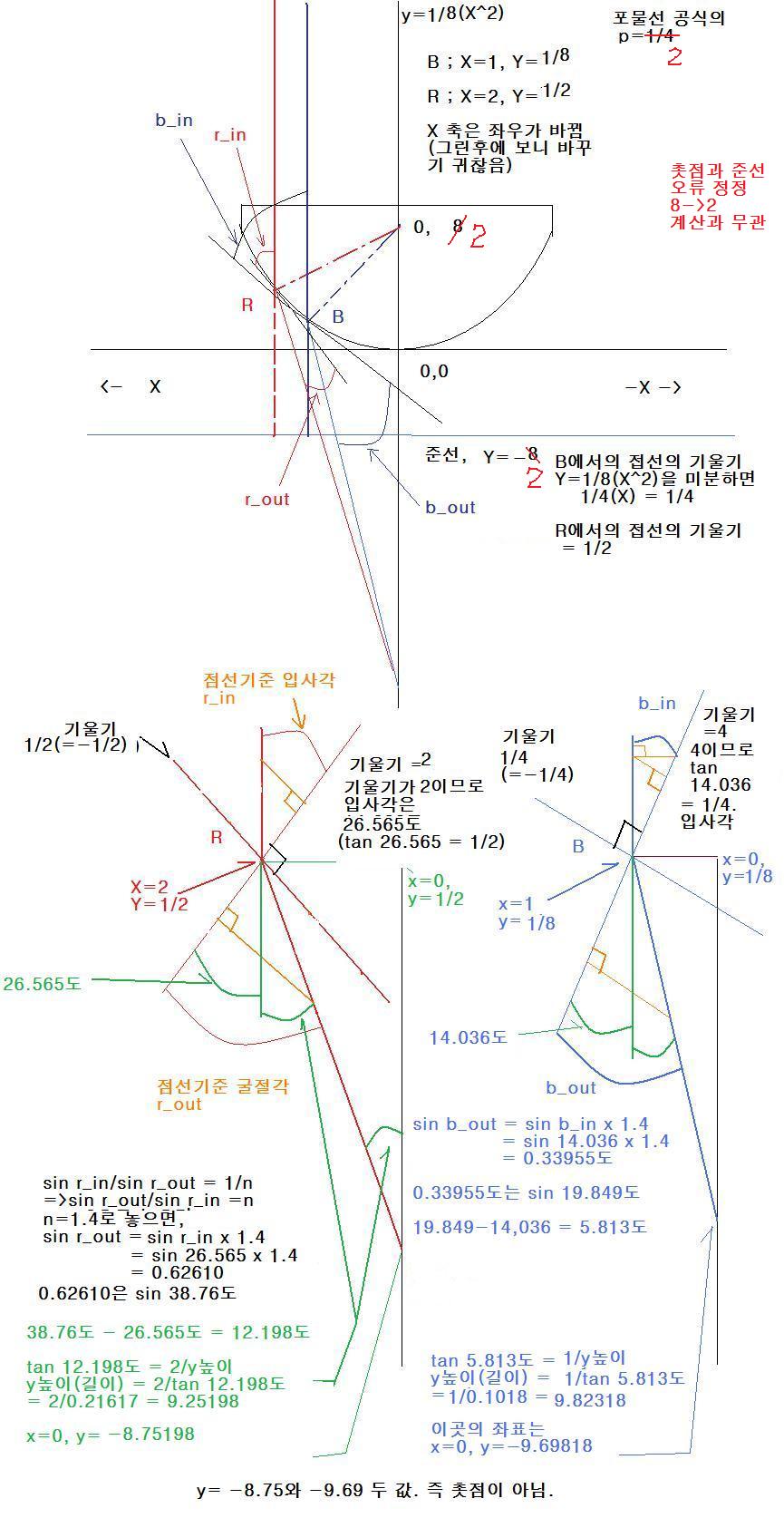
21일 23시 18분 추가

위의 차이점은 원인을 찾았습니다. (입사각이 너무 커서 전반사 근방이어서  그렀습니다.

다시 각도를 줄여서 그려보아도 많이 차이 납니다.   굴절면은 포물면을 쓸수 없나 봅니다.

(붉은숫자 정정 8. 1/4 -> 2 은 22일 11시54분)

 

 

 -

22일 0시3분 추가.

그림의 수치 접어두고, 생각(굴절, 반사 등)을 해보니 굴절주경에는 굴절법칙 때문에 포물면이 의미가 없네요.........

굴절법칙과 매칭되는 특정 변수값의 함수가 있을수가 있고(예를 들면, X항이 있던가, X의 세제곱항이 있던가 등등, 이건 내 능력밖 ㅎㅎ) 

-

22일 11시55분 추가.

굴절면이 2곳(위에서는 편의를 위해 1곳만 굴절되는 조건으로 게산했습니다)이 어떨까(보정이 되지 않을까 등) 생각드는데,,,,,

망원경 가공용 프로그램을 어디서 듣기는 들었는데(천망동?)프로그램에 포물면값도 넣을수 있다면 금방 판명은 나겠지요^^

-

23일 3시26분 추가

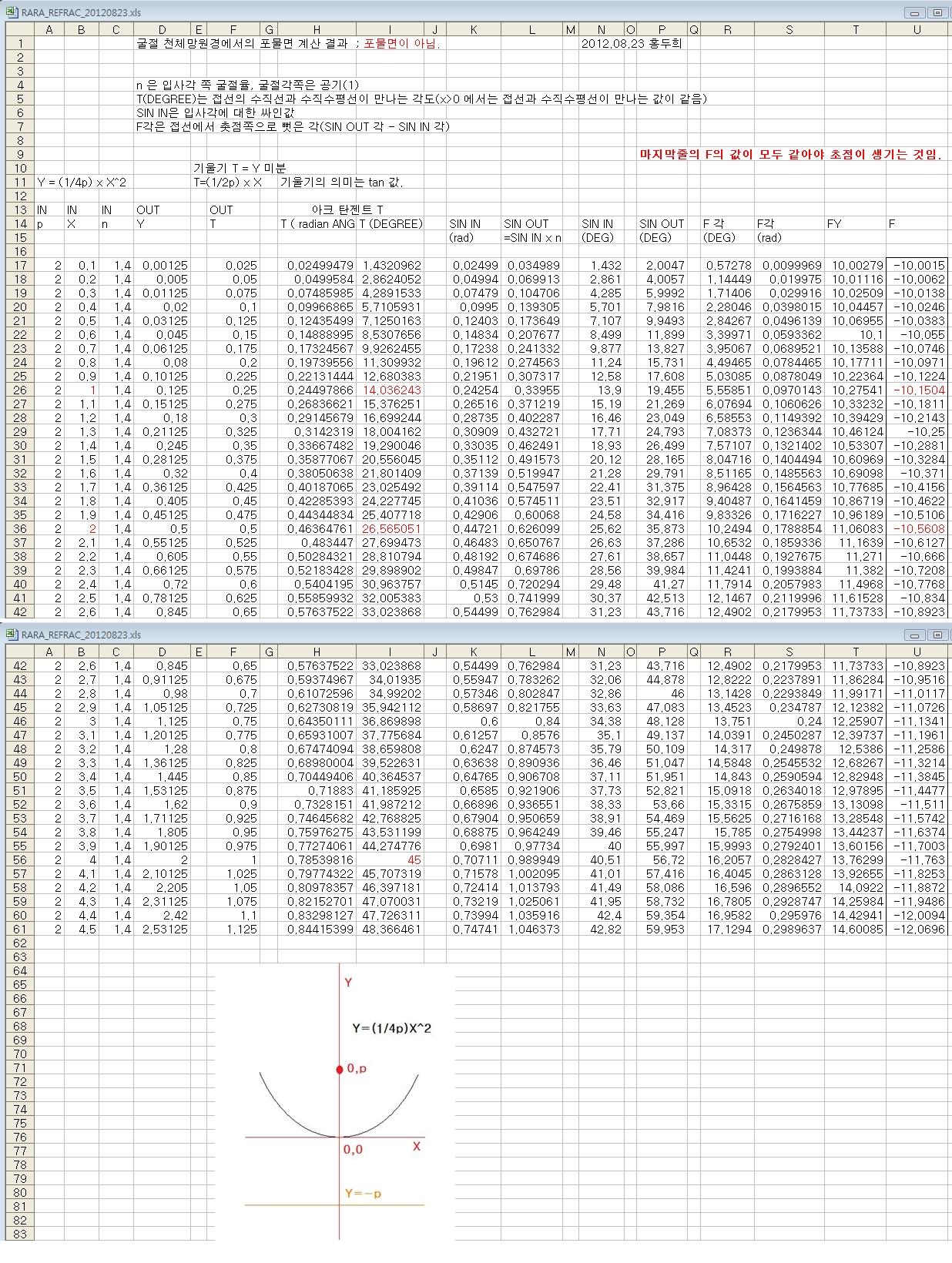
밤 12시 쯤부터, 엑셀로 표를 만들어 봤습니다.

sin out = sin in X n(굴절률) 로 부터 이상하게 막히더니 결국 저의 어제 계산 방법에(사인값의 차이를 그냥 각도의 차이로 혼돈하였음)

오류가 있었습니다. 지금 계산검증이 아니었다면 나중에 챙피했겠지요^^

첨부 엑셀 화일 ; PARA_REFRAC_20120823N.XLS

 

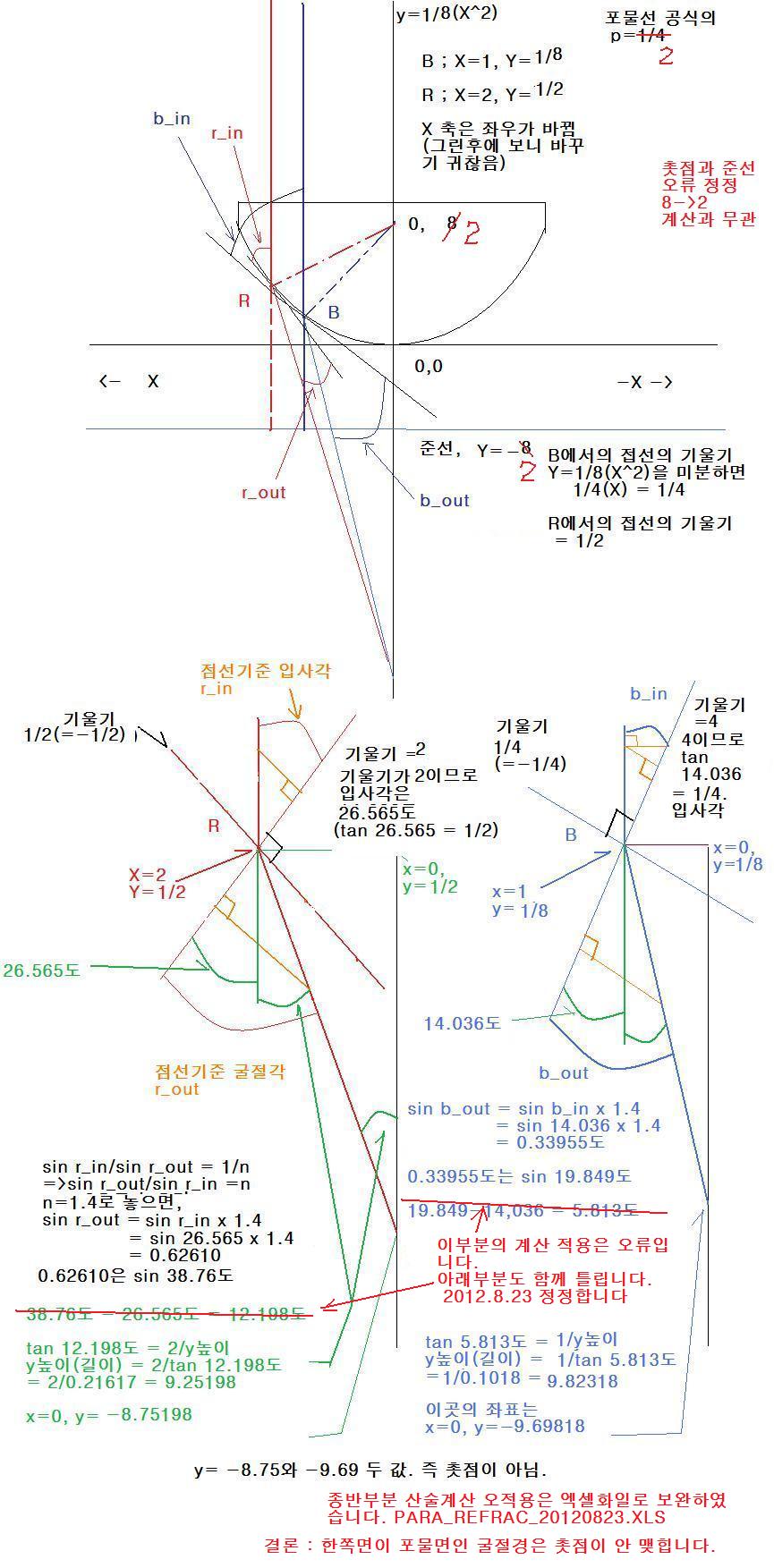
결론은 굴절경은 포물면(저의 검증은 한쪽은 평면이고, 다른 한쪽은 포물면)이 아닙니다.

 

 

 

  -

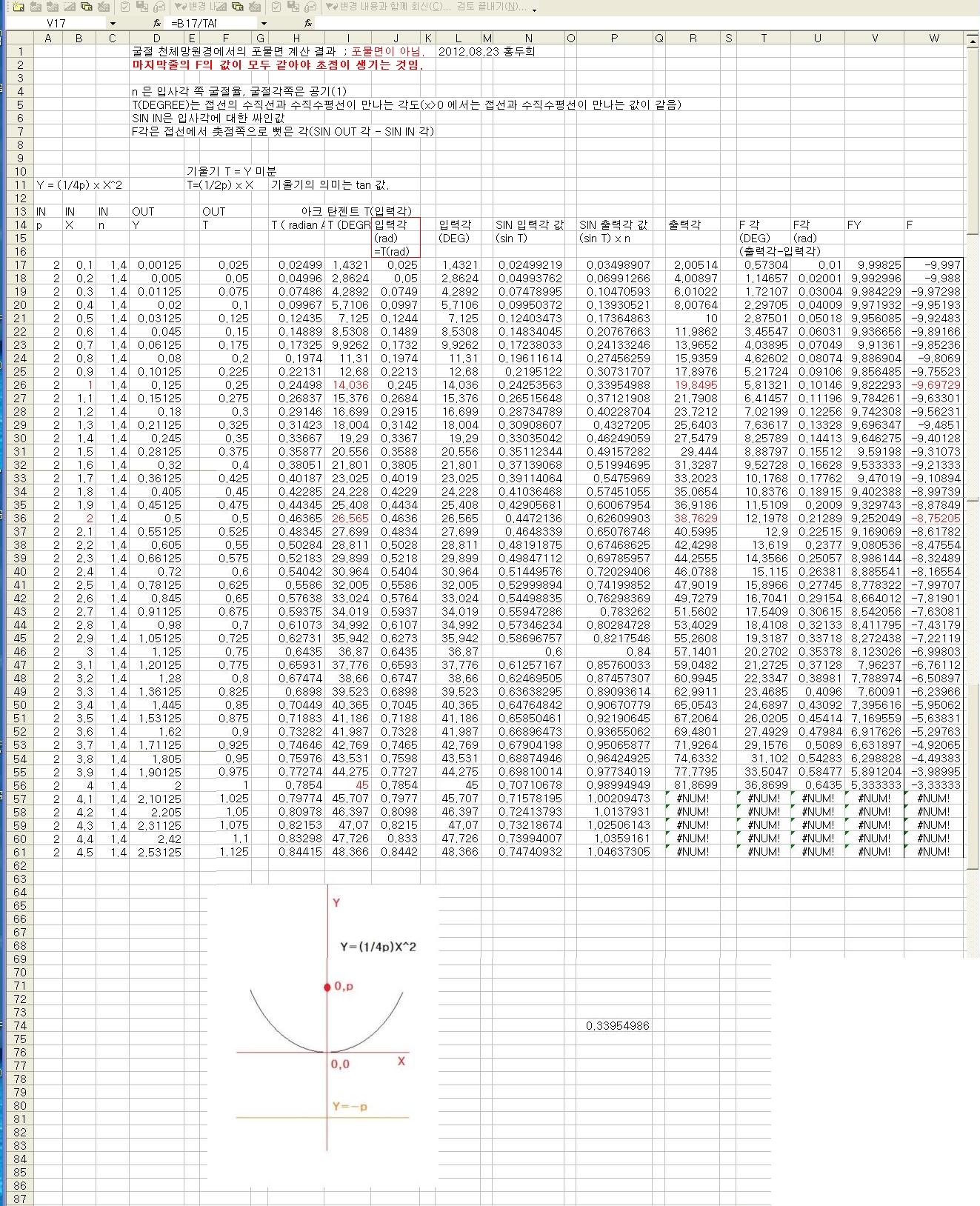
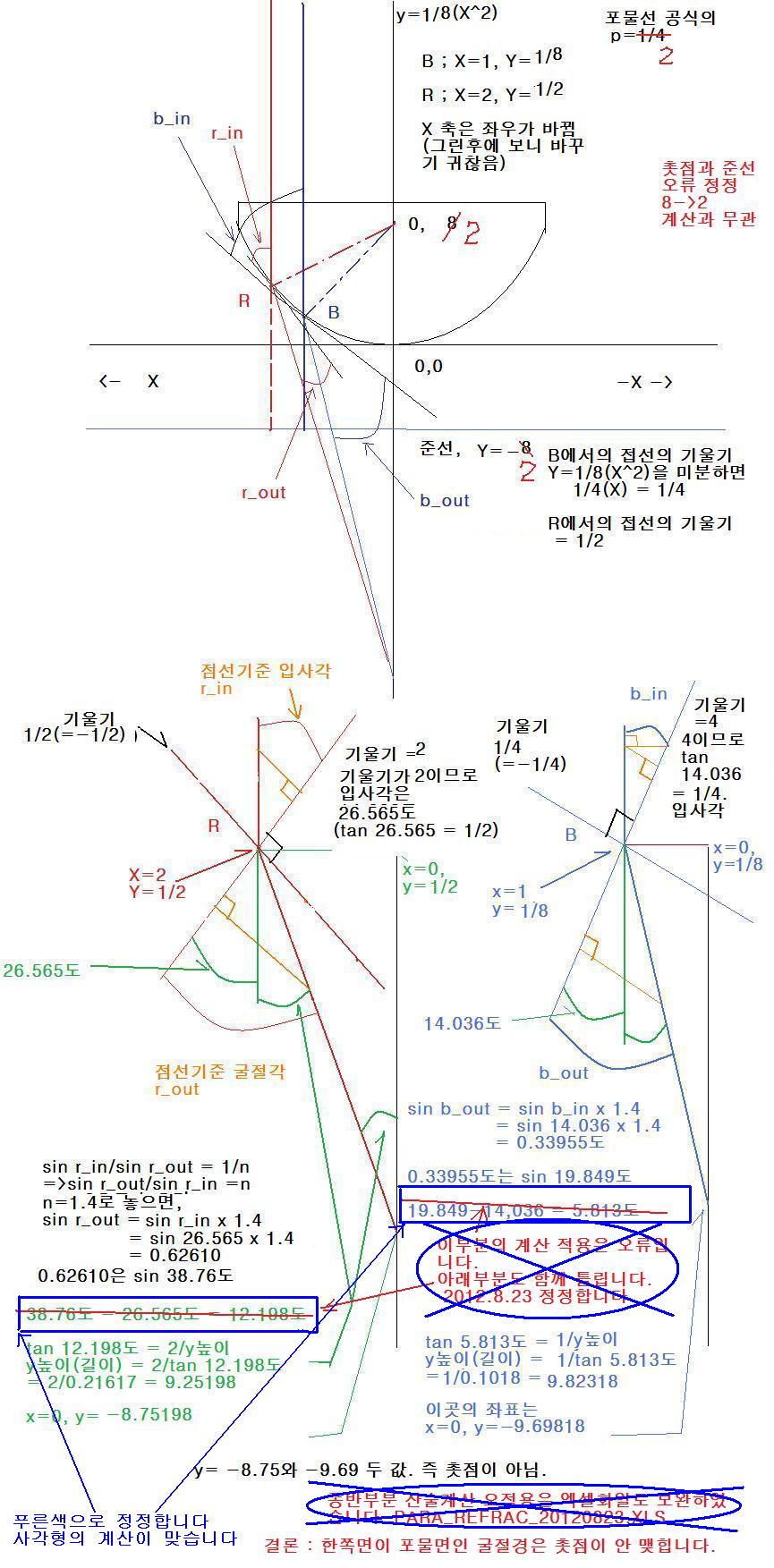
23일 14시48분 오류를 수정합니다. 결론은 같은데 계산과정에서 틀린부분(tan 적용부분과 sin 적용부분) 오류를 잡았습니다.

계산기로 계산한곳에서 오류인줄 알았으나(오늘 새벽) 작도와 계산기 부분은 맞는 방법이었습니다.

오늘 새벽에 엑셀로 만든 차트에서 오류가 있었습니다.(tan 부분과 sin부분에서)

위의 틀린부분을 그냥 놔두겠습니다^^

최종 엑셀화일과 그림을 첨부합니다. para_refrac_2012-823Nn.xls

 

 

 

 -

2012년 8월24일 18시20분 추가.

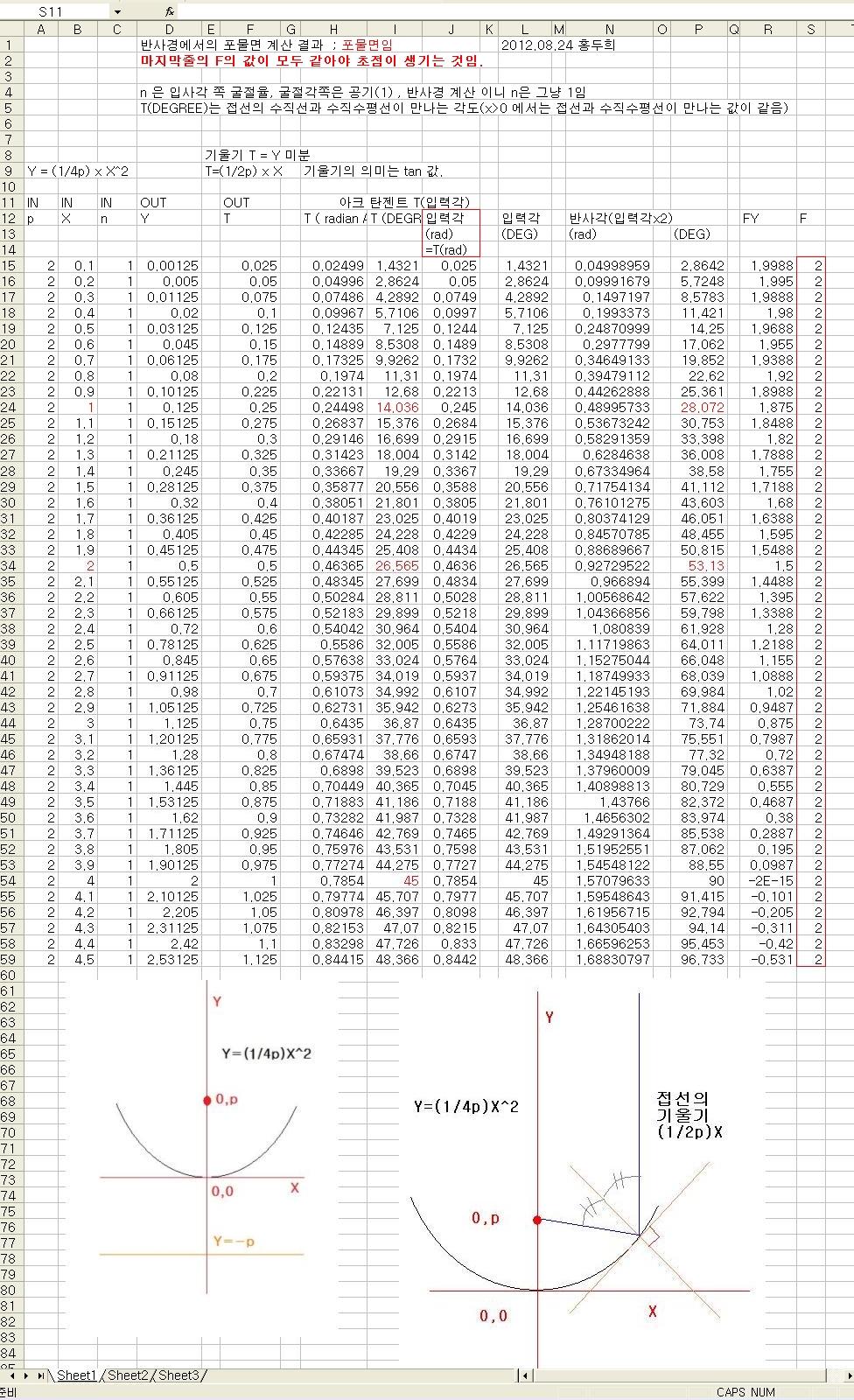
제가 몇년전에 포물선 반사의 촛점이 생기는 것을 이곳에 종이에 끄적였습니다. 아마 그때도 게산기로 2포인트를 계산해서 동일한 지점을

지나는 것을 어렵게(ㅋㅋ) 겁증한것 같은데, 이번 기회에 엑셀로 돌려봤습니다.

촛점이 나옵니다^^

포물면에선 촛점이 생깁니다 ㅎㅎ, xls 화일은 첨부 안합니다 ㅋㅋ