네 또 그 타령입니다.
도서관에서 책을 빌려왔는데 아무래도 소장용을 사야 하겠습니다.(프린키피아,과학의 탄생 이후 3번째)
경문사의 수학의 천재들인데 아무래도 잘 쓴 책입니다. 알짜를 모아 모아 놓았습니다.
파르마의 마지막 정리가 증명(95년)되기전인 90년에 쓴 책인데 제게 딱 맞습니다.
유클리드에 대한(내용) 설명에서 고전의 위대함을 느꼈습니다. 책을 설명(저는 어쩔수 었이 책을 설명한 책을 번역한 책을 봅니다 ㅊㅊㅊ)하는
책을 잘 골라야 하는 것이 무척 중요하다고도요.
유클리드의 책(유클리드의 원론)에는 피타고라스 정리가 나옵니다. 물론 유클리드는 책에서 이미 알려진 방법대로 증명을 기록했습니다.
유클리드가 이 증명 다음에 기술한 증명(순서대로 번호를 매겨 놨습니다. 나중에 증명하는 방법에는 앞서 증명된 결과만을 이용해야 합니다,
우리가 수학 문제를 풀거나 증명할때는 이런 순서를 전혀 고려할 필요는 당연히 없지요)이 저를 고전의 위대함을 느끼게 합니다.
그 증명의 주제는 피타고라스 정리의 역입니다..... 이런 철저함이 수학의 뿌리가 되는 거지요.
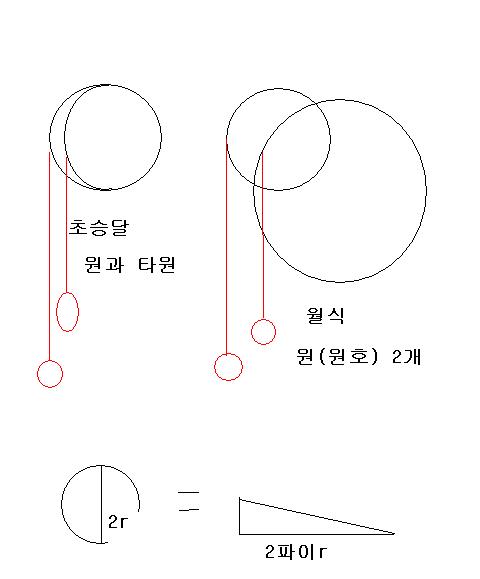
얼마전에 그믐달을 보며 타원을 알게(^^) 되었는데 월식때의 2개의 원(원호)도 기억에 남고요.
책에는 2개의 원호로 이루어진 도형이 나옵니다. 원주율을 알기위한 도구로 사용도이었습니다.
제가 그동안 책에서 본것은 원주율은 원의 내접과 외접 정다각형의 수를 키우면서 시작되었고
수열을 이용해서 쉽게 계산을 할수 있다고 보아 왔습니다. 내외접 정다각형의 방법의 아이디어가
2개의 원호부터 시작하는 것을 이 책을 알게되었으니 어찌 기쁘지 아니 하겠습니까.
중학교인지 초등학교부터 전자 계산기를 보며 신기했었습니다. 가감승제야 주판알를 튀겼으니
전자장치로 주판알 처럼 올려주고 내려주고 전자기계가 해주는 것으로 이해해서 별로 기기하다고
생각하지는 았았지만 루트는 참 이상했습니다. 루트가 이렇게 쉽게 빨리 답을 튀어낼수 있나?
신기하지만 이해 안되는 것이 어디 한두가지 입니까? 그냥 그냥 머리속 저곳에 집어 넣어 두었고
일주일에 한두번은 계산기 화면을 보면서도 기술자가 알아서 잘 했겠지했습니다.
뉴턴이 루트를 아주 쉽게 게산하는 방법을 알아냇다고 합니다. 참 대단합니다. 아마 싸구려 계산기속이나
슈퍼 컴퓨터에서도 아직고 그방법으로 하고 잇을겁니다. 다른 방법이 있다면 이 또한 저의 관심사지요.
웨스트민스터 사원에 또 가야 되겟습니다. 책을 읽다보니 뉴턴의 무덤근처에 다윈의 무덤도 있다네요,,,
-
27일 0시45분 추가.
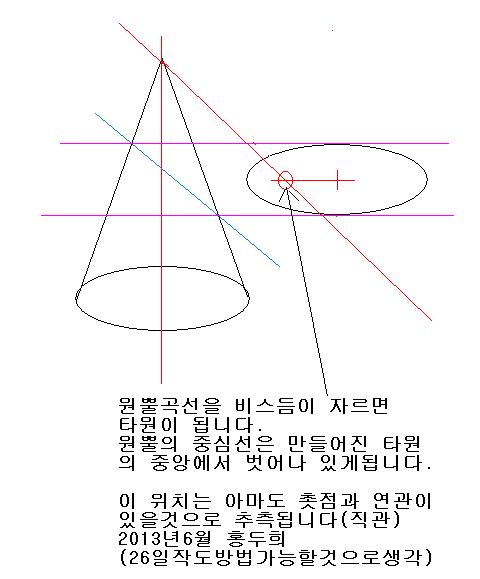
타원을 생각하다가 원뿔곡선에서의 타원에서 10여일 전에 이런 의문이 있었습니다.
원뿔곡선에는 특별한 포인트(선,점)가 있습니다. 바로 원뿔의 중심입니다.
원뿍곡선의 원의 중심은 바로 원뿔의 중심입니다.
그럼 다른 곡선(타원,포물선,쌍곡선)에서 원뿔곡선은 무슨 관계일까라는 생각이 며칠후에 들었습니다.
갑자기 이 생각이 들응 것은 아닙니다. 그동안 이렇게 만들어진 타원을 어떻게 수학적으로 기술할까를
책을 안보고 제 머리속에서 생각하는 도중이었으니까요. 3차원 입체를 3차원으로 자른후 만들어진
비틀린 2차원 타원의 그래프 수식은 제 머리속에서 감이 안 왔습니다. 이렇게 며칠을 보낸후에
이 생각이 들은 겁니다. 중심은 분명히 특별한 점일 것이다......
제가 추측하건데 아무래도 촛점과 관계가 있을 겁니다. 증명을 해야하는데 수식을 만들수 가없으니 어쩔수 앖었지요.
오늘 전철을 타고 가면서 생각하니 답(그래프를 그릴수 있다)이 나옵니다. ㅋㅋㅋ.
-
2016년7월10일 추가
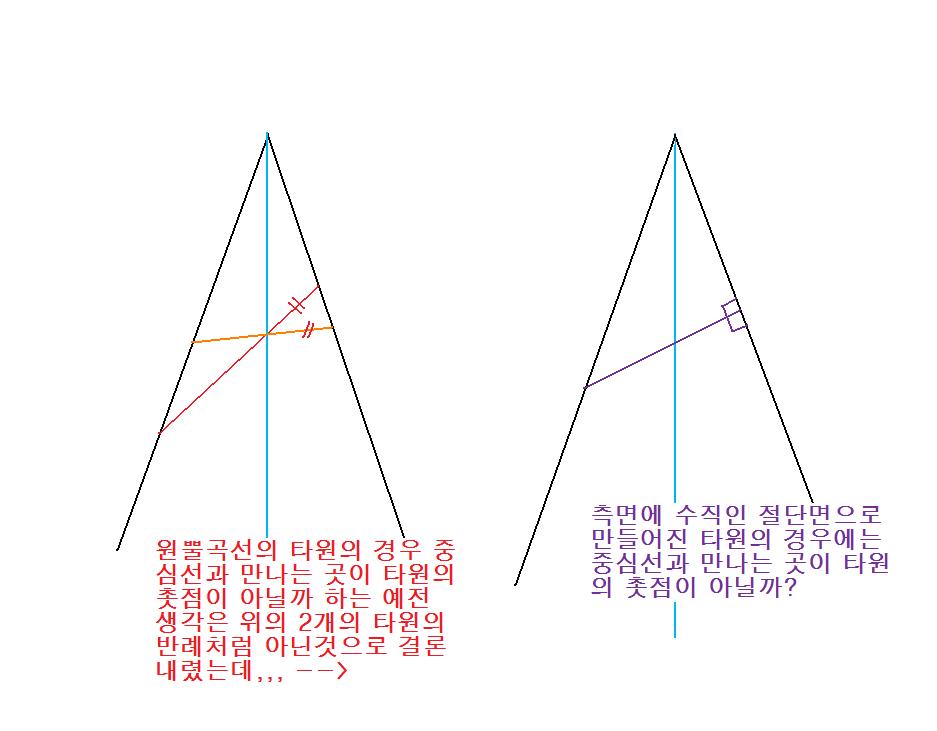
바로위의 원추곡선에서의 타원과 중심축이 만난는 곳이 타원의 촛점이 아닐까 하는 생각은 글 작성일(2013년6월) 이후
촛점이 아닌 반대의 예를 알아서 이곳 게시판 어디에 쓴 기억이 있습니다.
오늘 다시 생각을 추가하며 예전 생각도 첨부 합니다.
즉 무조건 촛점이 되지는 않습니다.
그렇지만 특별한 조건에서는 촛점이 될수도 있다는 생각이 들었습니다. (아래 그림의 오른쪽)