아까(2014년 9월 18일 0시쯤),
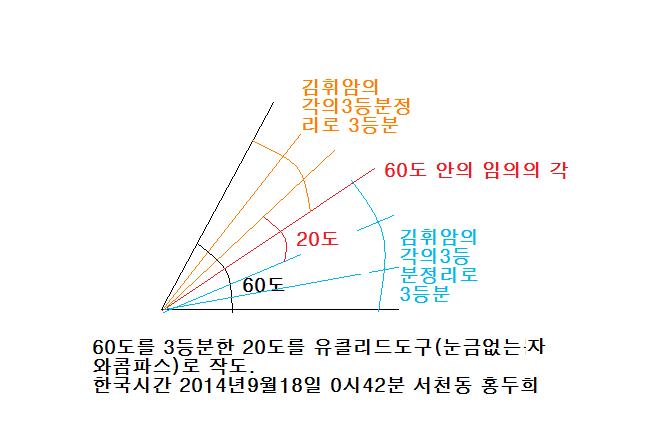
그동안 풀수 없다고 책에 적혀있는 문제(60도를 3등분 하기, 즉 20도 만들기, 유클리드도구만 가지고(눈금없는 자와 콤파스))가
풀린것 같습니다.
김휘암님의 책 '각의 3등분의 정리' 후반부를 보다가 생각이 났습니다.
저자의 책에도 60도는 유클리드 도구로 3등분할수 없다고 하셨는데,
김휘암님의 정리(각의 3등분의 정리)를 아주 간단한 방법으로 적용하면 3등분이 되네요.
원에 내접하는 9각형도 유클리드도구로도 그려지는 겁니다.
그림은 2014년9월18일 0시42분에 그렸으며 지금 서천동 홈페이지에 올린 시간은 18일1시6분 이네요^^
내일 김휘암님께 연락 드려야 겠습니다
-
5시9분 추가
앞 사무실 아저씨에게 검사 맞으러 갔더니 뻘소리 하지 말라고 합니다. OTL. OTL.
정리에 오류가 있답니다....
인과 관계 전도의 오류라고, 정리를 논증하면서 3등분을 가정하고 시작했는데 이러면 안된다고 하네요....
즉 말하자면 어떤각 을 삼등분한 것이 a라고 하면 처음의 각은 (당연히) 3a일 것이고 3a라는 각이 있을 때 그
3등분된 각 a의 존재를 가정한다는 것은, 각의 3등분의 문제가 아니고 3배각의 작도문제가 된다는 것이라네요.
어떤 임의의 각의 3배각의 작도는 당연히 가능한 것이고, 김휘암님의 논증은 결국 3등분각의 작도가
아니고 3배각의 작도 문제가 된다는 거지요.

 소현이 엄마입니다^^
소현이 엄마입니다^^
두분 무슨 대학 원로 교수님들 같습니다? ㅎㅎㅎ