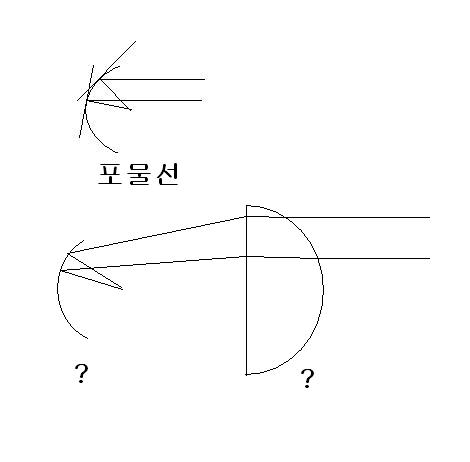
수평광이 한 점에 모이는 촛점을 몇년전에 고민한 후에(같은 곳을 지나고, 같은 거리가 걸리는)..
오후에 길을 걷다가 생각이 또 납니다. 비슷하지만 다른 생각들....
1. 포물선의 방정식인 y^2 = (4p)x, 4p는 상수.에서
1-1 이것 말고 다른 방정식은 없을까?
1-2 수평광이 한 점에 모이는 (곡선)함수의 일반식을 표현할수 없을까?
곡선위의 한점에서의 미분은 그 곡선의 기울기를 나타내고,
그 점을 지나고 그 기울기인 직선을 접선이라고 하기때문에,
임의의 점(일반방정식이 만들어지면 그점이 곡선)에서 곡선위의 점으로 향하는 새로운
직선이 접선과 이루는 각의 반사각이 수평이라면 그 곡선은 수평광을 한점으로 모을수 있겠네요.
두가지(같은곳과 같은 거리)를 다 만족해야 하고요.
1-3. 곡선이 1개가 아니고 2개또는 그 이상일때는 최소의 춧점(추정)으로 부터 최후의 수평광까지의
관계가 형성되면 새로운 광선모음 광학계~~.
(타원과 쌍곡면은 아마도 이런 원리가 적용된것 같습니다. - 제가 아직까진 타원과 쌍곡선을
고민하지 않았습니다.,, 지금부터 랄랄랄랄.)
쉽게 보는 보정판이 이 원리라고 생각되는 일반해를 알고 싶어서~~
