몇년전부터 가져왔던 위문이 얼마전에 끝난 것으로 생각했는데, 다시 의문이 살아 났습니다.
간단히 정리하면 이렇습니다.
원추(원뿔)곡선을 칼로 베어낸 단면을 보면 원(원반),타원(면),포물선(면),쌍곡선(면)이 나옵니다.
원추곡선의 중심을 지나는 가상의 선을 생각해보면, 이 선과 위의 면이 만나는 점이 있게 됩니다.
저는 이 점이 타원(포물,쌍곡은 타원이 끝난후 생각합니다)으 촛점이 아닐까 생각이 들었습니다(4년여 전부터)
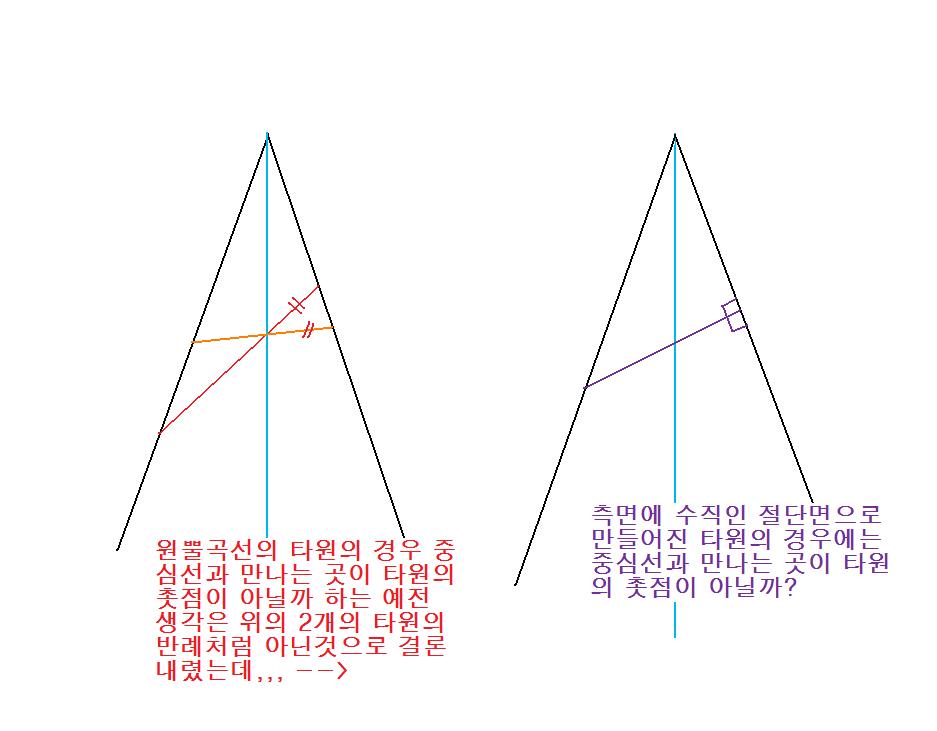
그러던 중에 아래 그림의 왼쪽처럼 얼마전(이곳 게시판 어디에 끄적였습니다, 지금 못 찾겠네요)에 촛점이 될수 없는
예를 찾았기 때문에 그만 종료 헸었습니다.
3일전에 버스를 타고 가다가 그 생각을 좀더 이어갈 필요가 생겼습니다.
오른쪽 그림처럼 어떤 특정한 조건에서의 타원이라면 가능하지 않을까?
이번의 경우는 사고실험이 아니라 작도나 연산으로 풀수 있을것 같습니다. ㅎㅎㅎ.
-
13일 3시 추가
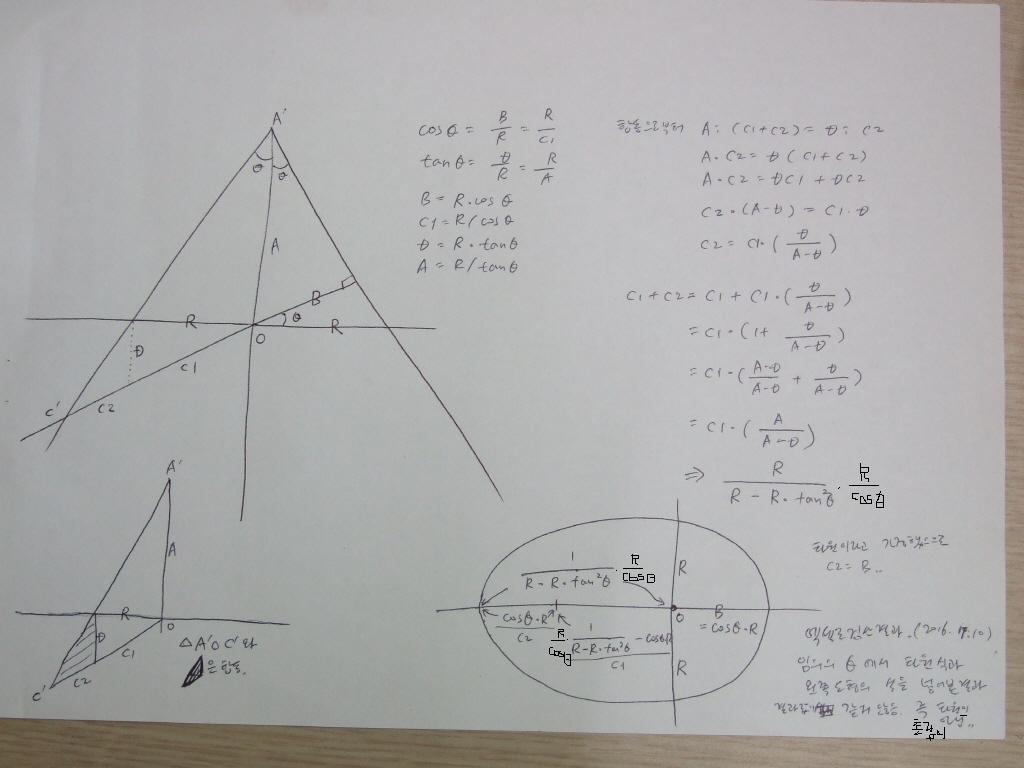
어제는 위 도형을 3개의 직선으로 표시된 1차 방정식으로 놓고( Y = 기울기 * X + C ) ,두개의 직선이 교차하는 지점의 죄표로 부터
각각의 거리를 게산해 보았습니다. 세타를 30도로 놓고(편하게 계산하기 위해) 해보니 초점으로 가정한 값이 안나옵니다. 즉 촛점아님
직선으로 전개한 1차식이 훨씬 간단하네요.



