우리가 학교에서 수학과 과학을 배운것은 거의 최종본 입니다.
뉴턴의 프린키피아 번역본을 보아도(현대 언어와 수식으로 순화를 해놓아도) 일목요연하지 않은 기분이 듭니다.
그럼에도 유명한 것이라고 하니까 그런가 부다 했습니다.
뉴턴이 미분을 이용할 수 있었던 것은 아마도 대수방적식이 보편적으로 알려져있고, 곡선을 표현하는 쉬운 수학 도구가 개발 되었을 것입니다.
저는 수학사에 문외한 이라서 언제 어느 수학 도구들이 만들어 졌는가는 미적분에 관한 두분의 논쟁말고는 아는것이 없습니다.
그래서 뉴턴이 거인 어깨 이야기를 하신 것이 겠지요.
y=ax^2 이라는 것이 포물선을 표현하는 수식인데 수식이라는 용어와 표현등이 어느시대 부터 있었던 것은 모르고요.
뉴턴은 아마도 x, y 제곱근등 수학적 표현이 보편화된 때에 살았던것 같습니다.
그리어 그것을 자르고 붙여서 미적분을 생각한것이 겠지요.
원뿔곡선읜 2000년도 전에 알려 진거랍니다 (아폴로니우스 의 원 / 원쁠 ..)
이런 의문이 들었습니다.
그때에도 촛점이 언급 되었을까????
아마도 아닐겁니다. 아니 최소한 한두개는 빼고.
어떤 곡선의 특별한 한곳 또는 두곳의 포인트가 아주 특이한 현상을 가진곳을 촛점이이라고 하면
즉 포물선의 경우 촛점은 포물선(면)에서 반사된 직선이 한곳을 같은 거리만큼 걸려 지나는데
반사를 하려면 곡선의 기울기를 알아야 하는데 곳선의 기울기가 미분이지요,
미분이 나오기 전에는 기울기를 알수 없는 거고요.
1800년대에 어떤 수학자가 드디어 우리가 알고있는 원뿔곡선의 일반적인 표현방법을 알았다니 ,,,
저는 그래서 기쁩니다.
어제 어느 출판사에서 전화가 왔습니다.
저는 늘 하던대로 시큰둥,,,
완주별잔치에 책을 보내준답니다.
통신상의 기억력 때문에 문자로 보내주실 책들과 출판사를 알려달라고 했습니다.
잠시후 문자가 왔습니다.
저도 고마운 마음을 글로 표현을 해야해서 답장을 썼습니다
감사 등등
그리고 마지막에 상투적이지 않은 내용을 뭐러고 쓸까 잠시 생각한후 이렇게 썼습니다.
'먹다 지쳐 잠이드는 것이 아니라 책을 보며 잠들면 저는 좋습니다. 눈뜨면 바로 글이 보이니까요'.
ㅎㅎ 제가 홍천에서 마당에 전기장판위에 담요덮고 얼굴만 내밀고 자는 이유와 같지요.
-
어젠 저녁에 재욱님이 들렸습니다.
이퀴 플랫폼과 16인티 돕소니언을 장만 했다네요.
이퀴 플렛폼 이야기가 나왔습니다.
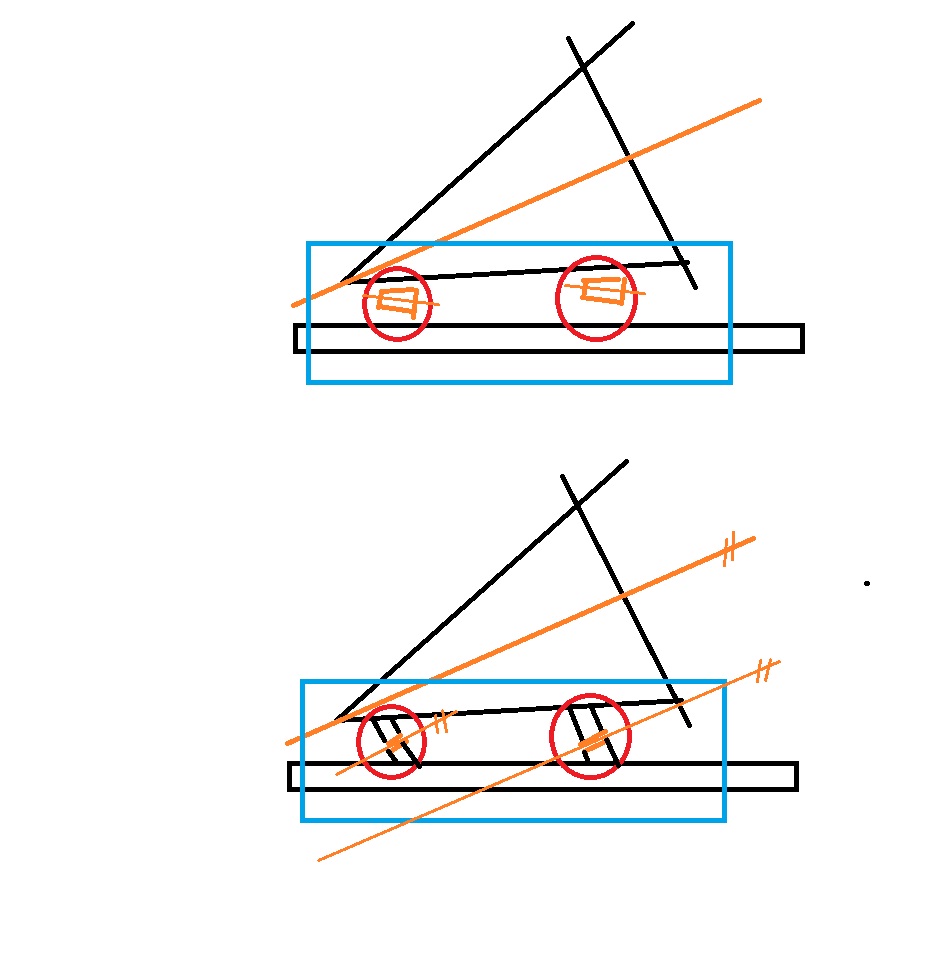
아래 사진에서 원뿔면(상판)과 밑판의 접합면(평면)의 모양이 달라서 미끄럼짐이 발생할수 있습니다.
아래의 경우처럼 원뿔면을 원통면으로 만들면 모를까.
정석은 밑판의 로울러를 태이퍼지게 해야지요.
-
11 월 8일 0시2분 추가
거인의 어깨입니다.
영문 위키피디아에서 갈무리 했습니다.
스넬의 법칙은 1621년
Although named after Dutch astronomer Willebrord Snellius (1580–1626), the law was first accurately described by the scientist Ibn Sahl
at the Baghdad court in 984. In the manuscript On Burning Mirrors and Lenses, Sahl used the law to derive lens shapes that focus light
with no geometric aberrations.[1][2]
The law was rediscovered by Thomas Harriot in 1602,[7] who however did not publish his results although he had corresponded with Kepler
on this very subject. In 1621, Willebrord Snellius (Snell) derived a mathematically equivalent form, that remained unpublished during
his lifetime. René Descartes independently derived the law using heuristic momentum conservation arguments in terms of sines in
his 1637 essay Dioptrics, and used it to solve a range of optical problems. Rejecting Descartes' solution, Pierre de Fermat arrived
at the same solution based solely on ~
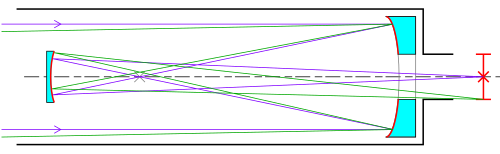
뉴토니안 전인 그레고리안은 1663년
뉴토니안은 파라보라로 1667년
Gregorian[edit]
The Gregorian telescope, described by Scottish astronomer and mathematician James Gregory in his 1663 book Optica Promota, employs a concave secondary mirror that reflects the image back through a hole in the primary mirror. This produces an upright image, useful for terrestrial observations. Some small spotting scopes are still built this way. There are several large modern telescopes that use a Gregorian configuration such as the Vatican Advanced Technology Telescope, the Magellan telescopes, the Large Binocular Telescope, and the Giant Magellan Telescope.
Newtonian[edit]
The Newtonian telescope was the first successful reflecting telescope, completed by Isaac Newton in 1668. It usually has a paraboloid primary mirror but at focal ratios of f/8 or longer a spherical primary mirror can be sufficient for high visual resolution. A flat secondary mirror reflects the light to a focal plane at the side of the top of the telescope tube. It is one of the simplest and least expensive designs for a given size of primary, and is popular with amateur telescope makers as a home-build project.
The Gregorian telescope is a type of reflecting telescope designed by Scottish mathematician and astronomer James Gregory in the 17th century, and first built in 1673 by Robert Hooke. The design
pre-dates the first practical reflecting telescope, the Newtonian telescope, built by Sir Isaac Newtonin 1668,[1] but was not successfully
built until five years after Newton's first reflecting telescope.


 2016 올해의 천문인 , 300,000
2016 올해의 천문인 , 300,000
 감사 1300 (추가 = 7 x 50 + 7 x 50 + 12 x 50 )
감사 1300 (추가 = 7 x 50 + 7 x 50 + 12 x 50 )
그레고리안이 뉴토니안보다 먼저라는게 놀랍네요
그레고리안 흉내내보려고 하는 참이었는데...사실 카세그레인으로 테스트해볼 마땅한 부경이 없어서
어쩔수 없이 6인치 막스토프 주경을 부경으로 사용해볼 생각입니다
어쩔수가 없어서요 ^^;;
주경은 미드에서 만든 16인치 F1.2 테라빔용 미러이고 부경은 징후아 MC152 주경으로
위에 회장님 미분설명에 나온바에 따르면 F1.2 주경에 사용하려면 부경이 F2정도여야 하는데
최적인것은 삼양 500미리 F6.3에 들어있는 주경일것 같은데 징후아것도 비슷할것 같습니다
글 하나에 제가 구상중인 내용이 이렇게 많이 튀어나오다니 재밌네요 ^^
그리고 사장된 광학 기술이 아니고 대형 망원경에 사용되고 있다니 힘이 됩니다