2016년 1% 지난 기념으로 고문을 시작 합니다.
몇년동안 생각하던 것이 오늘 오후 앞 사무실(지하로 작년에 이사) 아저씨와 이야기 하던중에 풀어 주셨습니다(제가 푼거 아닙니다).
지구와 부닥치는 천체(유성, 위성, 소행성, 혜성)의 최대 속도에 관한 내용 입니다.
일단 제가 어제까지 생각했던 내용은,
지구와 부딛치는 천체의 속도는 지구공전 속도의 2배는 넘지 않을 것이었습니다.
천체가 타원,포물선,쌍곡선으로 지나가다가 지구궤도를 지나가는 지구와 부딛친다면
태양-지구의 거리와 태양-천체의 거리가 같기때문에 그 포인트에서는 같은 속도를 가질것으로 보았습니다.
타원 천체의 경우 1년에 한번 주기로 태양을 돈다면(지구도 1년에 한번) 지구 바깥에서는 지구보다 천천히
돌것이고, 지구 안쪽에서는 지구보다 빨리 돌며, 지구와 같은 거리에서는 지구와 같은 속도를 돌거라고요.
지구와 정면 충돌 한다면 충돌속도는 지구 속도의 2배가 될것이고, 지구 뒤를 따라와서 부딛친다면 충돌속도는
0이 될테니까요. 어쨌든 타원 궤도 주기에 관계없이 지구 궤도에서 정면 박치기를 한다면 지구공전 속도의 2배이상은
안 나올거라고 봤습니다.
그런데 오늘 오후에 달라졌습니다. 2배이상의 충돌 속도가 나온다로,
낮에 앞사무실 아저씨가 잠시 생가하더니 지구 궤도에서의 속도가 지구 공전속도보다 빠르다고
그림을 그려줍니다. 헐헐헐
타원 궤도의 천체가 지구 궤도를 지날때에 타원궤도의 방향을 분해해보면,
'지구궤도 속도+태양방향의 속도'의 벡터합으로 나오기때문에 '태양방향의 속도'가 덤으로 빨라
(벡터합이니 그보다는 좀 작은)지는 것이지요.
이해를 좀 쉽게 한다면,
1년에 한번 타원궤도를 도는 천체가 있을때(아래 그림) 원일점에서는 천체의 속도가 지구공전 속도보다
느릴테고, 근일점에서는 지구 공전속도보다 빠르겠지요, 이때 천체가 지구공전 궤도상에 있을때는
어떨까 하는 겁니다.
지구궤도와 천체궤도가 만나는 지점에서의 각도에 따라서 속도가 결정될텐데 이 문제는 또 숙제네요.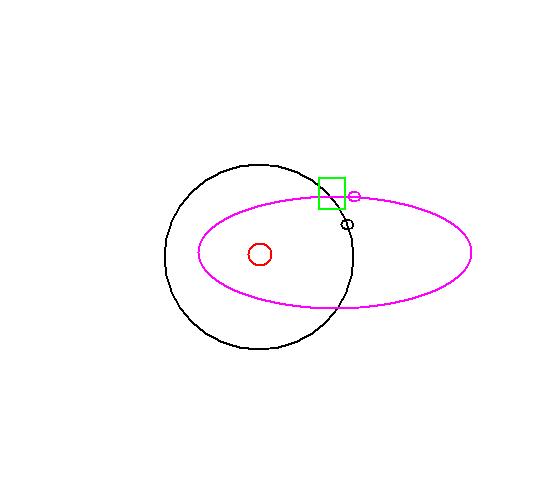

ps 케플러의 제3법칙
조화의 법칙
항성과의 평균 거리(궤도의 긴반지름)의 세제곱은 공전 주기의 제곱에 비례한다.
(위 그림의 빨강 태양과 지구의 평균거리(=1/2 * 지구의 근일점과 원일점의 거리)) = 1/2 *천체의 근일점과 원일점의 거리) 라면 공전주기는 같다.
-
5일 22시반경추가
퇴근하며 차에서 생각하니 천체의 최고속도가 얼마이하일것이 쉽게 계산됩니다 물론 근일점을 알고 있어야하고요
근일점에서 원운동을 하는 천체는 케프러 법칙으로 속도가 나옵니다
타원운동 천체가 근일점을 통과하면 그때의 속도는그위치에서원운동할때의 속도보다 느리게 됩니다 만일 속도가 같다면 원운동을 하게되는거니까요
속도가 느리니까 태양쪽으로 더 구부러져 가는거고 그게 타원인거고요 아무튼 이래서 타원천체의 최대속도의 범위가 좁혀지고 있습니다 ㅎㅎㅎ
물론 천체와 지구가 가까워지며 둘의 인력으로 속도가 빨라지는것은 고려하지 않고요

 등배파인더, 2월18일 추가, +21일, ++ 23일 9.7부능선 , -> 2월2...
등배파인더, 2월18일 추가, +21일, ++ 23일 9.7부능선 , -> 2월2...