아마 이것이 포물면의 아름다움과 연마의 기본을 위한 저의 3번째 생각인것 같습니다.
.첫번째는 포물면의 작도와 촛점면까지의 거리일치에 대한 생각.
.두번째는 포물면 가공을 위한 아이디어 차원에서의 가공기구 스케치.
이번에는 수학적 접근을 해보았습니다.
제가 늘 그랫듯이, 이번에도 모티브가 있습니다.
그저께(월요일), 일요일 내린 눈 때문에 대중교통을 이용해서 출근한 김준오님이 퇴근길에 들렸습니다.
제가 별보기 훨씬전에, 선두가 구의동에서 장사하기 전의 선두 사무실(동대문근처라고 했나??)에
가서(에플 컴퓨터 시절)반사경 연마 재료를 사서 12인치(10인치?) 인가를 연마 했다는 군요.
무거운 것을 겁없이 깍다 보니까 몸의 중심이 흐트러지고, 몸의 하중이 실려서 엉망이 되더랍니다.
그래서, 반사경을 매달아 놓고(인켈 큰 스피커통 2개를 이용해서) 몸의 하중이 실리지 않게
갈았답니다. 구면으로 먼저 갈았다는 거지요. 촛점 거리가 길어지면 구면이나 포물면이 비슷하기
때문에 초창기에는 구면으로 썼었다지요?
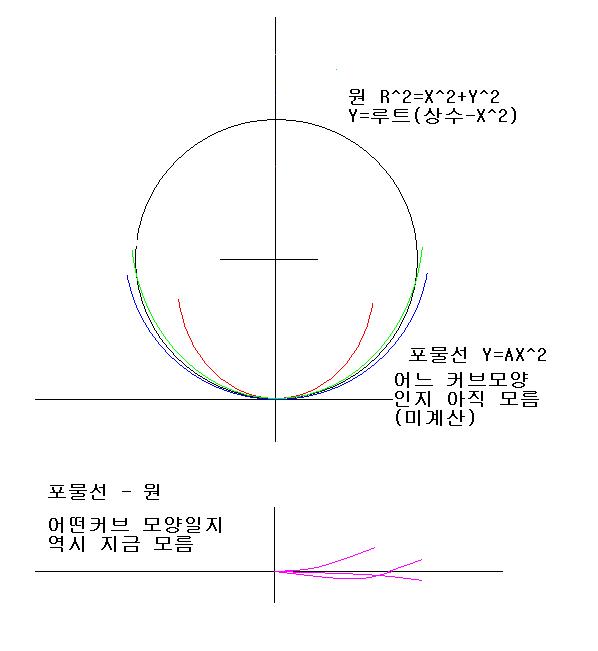
구면과 포물면의 차이를 수학적으로 계산해 보고 싶었습니다. "그리고" 수학적으로 끝나는 것이 아니라
그 "차이의 정량값"을 보정할 적당한 기구 장치를 생각하고, 만들어 보는 거지요~~. 마치 "캠-cam"처럼.
-
4시간 쯤후.
계산은 역시 안했음. 생각은 계속했음.
수학 함수를 그리는 프로그램은 알고 있음. 커브가 쉽게 그려져서 화면에 나오는 작은프로그램들.
한쪽 절편을 0으로 놓고 나머지 값을 구하는 '근의 공식'처럼 '포물선-[빼기]원을 하면 아래그림에서의
녹색 크로스선(+에서 -로 x축에서 한번 교차)의 값을 구할수도 있을 것임. '갈루아'의 근의 공식 증명처럼
근의 일반해가 있는지 없는지도 쉽게 판별될것 같음.








